.
This is equivalent to 
,
which explains the before mentioned exact difference of 1.The Golden Section is a well-known numerical ratio. If the sides of a rectangle have this ratio, it means that
the smaller is to the larger as the larger is to the sum of both. Numerically it is approx. 1.618034, or it's inverse
0.618034. Note the exact difference of 1 between these two numbers! It can also be defined as the solution to the
quadratic equation .
This is equivalent to ,
which explains the before mentioned exact difference of 1.
This ratio also shows up in the so-called Fibonacci Series. This is a sequence of numbers where each number is the sum of the two preceding numbers: 1 1 2 3 5 8 13
The ratio of two successive numbers in this sequence approximates the Golden Section.
A geometric visualization can be made as:
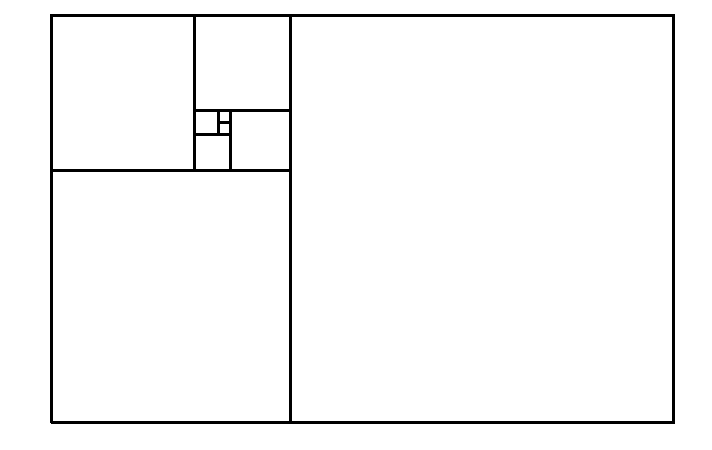
As I am very interested in the properties of odd numbers, I was looking for a generalization of the Fibonacci Series where the members would only be odd numbers. Of course this is very easily done by taking the sum of the three previous numbers: 1 1 1 3 5 9 17
Later I found out that such a series is often referred to as 'Tribonacci'.
The limit ratio of this sequence is the solution of the equation: 
, which is approx. 1.839286755. In closed form it can be
written as: 
. I took this as the aspect
ratio of my function movements.
A box can be made with this ratio: if the sides have length a, b and c, then a is to b as b is to c and as c is to a+b+c.
A visualization analog to the above figure can be seen in the next picture.
